Statistics is a branch of Mathematics and hence hated by many and actually it’s surprisingly unintuitive for many at first contact, including myself. Statistics is about expressing and calculating the chance of some events happening when there is more than one outcome that can occur. The standard example is rolling a dice. What is the chance of getting a “2”? There are 6 sides on a dice and one side of the dice is marked with 2 dots, so the probability is 1/6. This was the first and last detailed calculation in this post. I’m 90% sure 😉
In school everything seems so deterministic such that when students are first exposed to statistics it seems so useless and for many students statistics is the hurdle to their university degree.
As mentioned in an earlier post, I’m working on a chat robot, which is a program that can chat with you like a human would. My approach is that a computer is like a child that has to be taught very much to be able to behave like an adult.
In this process of modelling the learning behaviours of a human I see all kind of statistical and so called “machine-learning” methods which we humans use, but we are not aware of it. I would like to point out some examples and give you a motivation for learning statistics.
Let’s start with the babies: Infants are these helpless creatures lying on their back or belly and throw objects around if they are not putting them into their mouth. One reason why they throw objects is because they can’t control their movements, but throwing things has another effect: They find out that all object tend to come down to the ground. The knowledge of gravity pulling everything towards the ground is not hard wired in the brain and I guess children growing up on a space station would adapt very natural to the difference in how objects behave. And what makes you so sure that every object will be pulled down towards the ground? What makes you so sure that one day the stone that you throw will not just keep floating in the air? It’s because you have thrown many objects, really many.
Another example: Imagine kids around the age of 4-8 who are afraid of monsters under their bed. What makes you so sure that there will never be a monster under your bed? It’s because there hasn’t been any yet.
These examples are what in statistics is called hypothesis testing. We build a hypothesis and then we test it until we reached a point where we have tested the hypothesis often enough that we feel confident that the outcome is no coincidence. For example if you want to make sure that gravity pulls down a stone when you throw it, you just throw it many times. Let’s say you throw the stone 14 times and noticed that the stone hits the ground every time. The chance that this is a coincidence is 0,006% (Math note: assuming that a stone has no tendency to fall towards the ground, i.e. H0=”stone hit’s 50% of the time”).
So day by day you get more evidence that your hypothesis “stones always hit the ground” cannot be rejected. It’s important to notice that we can only “not reject” our hypothesis but we can never “confirm” a hypothesis, just like the problem with the gravity, we can never completely exclude the possibility that gravity decides to take a day of and everything keeps floating in the blue air.
Next statistical tool. You might have thought the following, when I wrote that “everything is pulled towards the ground”: What about balloons? They are not pulled towards the ground! Does that mean that gravity does not apply to balloons? Maybe (my experience is, though, that they fall to the ground when you puncture them).
What you do when you are thinking of those exceptions is that you are actually doing advanced mathematical modelling and you do it brilliantly!
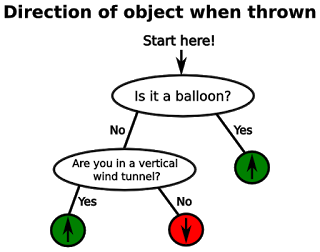
What you have build in your head is called a decision tree. A decision tree has a starting point with a question. For the gravity problem that might be: “Is the object a balloon?” And then you can go two ways: “Yes” or “No”. If the object that you throw is a balloon you pick the “Yes” way. The tree then either asks a new question or gives you an answer/decision. For example “Is pulled down by gravity” or “Is pulled up by gravity”:
We humans make uncountable decisions this way and even without having taken a course on that! Of course the tree above is very simple and gravity is not pulling up on objects. But wait! What makes me think that gravity does not pull balloons up? Try to answer that for yourself (not necessarily easy!)
Lets have a look at one more method before we conclude this post (more coming).
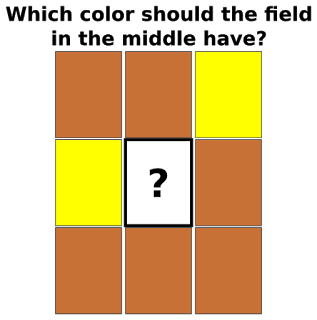
Let’s say you are a hiker and get to some fields. There is one field for which you don’t know the owner, but you know that farmer Joe owns the surrounding fields. Who do you think owns the field in question? If you are not trying to ask tricky questions, then you might have guessed that farmer Joe owns the field. Why? Because the neighbour fields are owned by farmer Joe. That method is called K-nearest neighbours. If we don’t have any more information, the best we can do is to vote on the majority. Take a look at this picture:
So what you do intuitively (maybe you weren’t even aware of that you are making decisions this way) is simply math.
Stay tuned for more models.
Comments are closed.